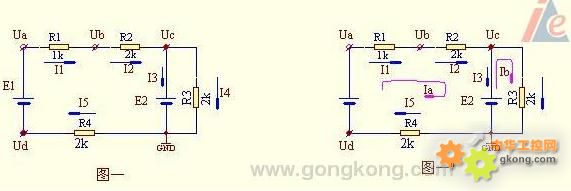
第1题 解答:已知:(1):E1=20V、E2=10V;(2):E1=5V、E2=10V;
一、 用含源欧姆定律求解 :
1、Uc对地的电压 = E2 =10V,向右看,可列:R3•I4 = E2 故可求I4电流:
I4 = E2 / R3 = 10 / 2 =5 A ……(1)(2)
2、Uc对地的电压= E2 =10V,向左看,可列:
E2 = E1 – R1*I1 - R2*I2 -R4*I5
该回路只有R1、R2、R4三个电阻串联,故可知:I1 = I2 = I5 = I 上式可简化为:
E2 = E1 –( R1 + R2 R4) * I
可得:I1 = I2 = I5 =I =(20 -10)÷((1+2+2))=2 A ……(1)
I1 = I2 = I5 = I =(5 -10)÷((1+2+2))= -1 A ……(2)
3、求I3电流:据克西克夫第一定律,可列:I2 = I3 + I4
I3 = I2 – I4 = 2 -5 = -3 A ……(1)
I3 = I2 – I4 = -1 -5 = -6 A ……(2)
4、求 a b c d 各点电位:
Ua=E1 – I5 * R4 = 20 – 3×2 = 14 v ……(1)
Ua=E1 – I5 * R4 = 5 –( -1×2) = 7 v ……(2)
Ub= I2 * R2 + E2 = 3×2 + 10 = 16 v ……(1)
Ub= I2 * R2 + E2 = ( -1×2) + 10 = 8 v ……(2)
Uc= E2 =10 V ……(1)(2)
Ud= -I5 *R4 =- 3×2 = -6 V ……(1)
Ud= -I5 *R4 = -(-1))×2 = 2 V ……(2)
二、回路法求解:设二个回路电流:Ia 与Ib 见图一”可列二个方程式
(R1 + R2 + R4)•Ia = E1 – E2 ……(1)
R3•Ib = E2 ……(2)
1、E1 =20V 求I1…I5 各电流值:
(1)式为:(1+2+2)•Ia = 20-10=10
得:Ia = 10÷5 = 2 A
(2)式为: 2•Ib =10
得:Ib = 10÷2 = 5 A
I1 = I2 = I5 = Ia =2 A
I4 = Ib = 5 A
I3 = Ia – Ib = 2 -5 = -3 A
2、E1 =5V 求I1…I5 各电流值:
(1 + 2 +2)•Ia = 5-10
得:Ia = -5÷5 = -1 A
2•Ib = 10
得:Ib = 10÷2 = 5 A
I1 = I2 = I5 = Ia =-1 A I4 = Ib = 5 A
I3 = Ia – Ib = -1 -5 = -6 A
3、回路法求a b c d各点电位同上一,故此处省略。
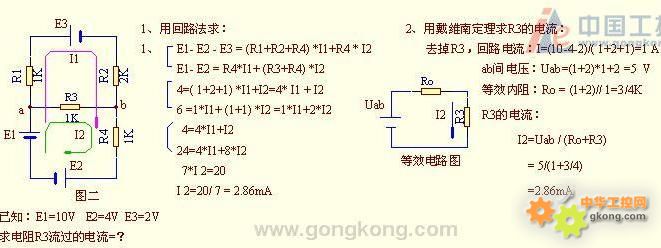
第2题解答:
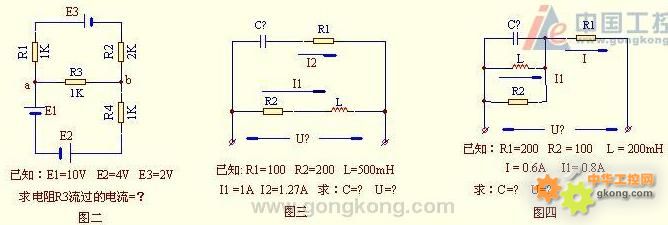
(注:图三为第3题,图四为第4题)
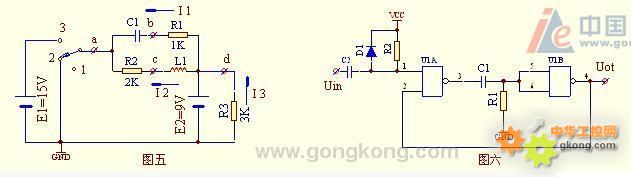
第5题 解答 :
这是一个过渡过程的问题,在分析电路之前,先复习一下L、C的有关特性:L是电流的惰性元件,在电路突变的瞬间,L中的电流不突变,它保持变化前的电流值再逐渐变化,而它的电压却可随着外界变化而变化,即可突变。C是电压的惰性元件,在电路突变的瞬间,C的电压不突变,它保持变化前的电压值逐渐变化,而它的电流却可随着外界变化而变化,即可突变。
一、见图五:开关指向2位,稳态时L相当短路,故 Uc = Ud =E2=9V。而C此时为开路状态,使R1的电流 I1=0,故Ub = Ud = 9V
此时a点接地,故: Ua=0V. I2 = (Uc – Ua) / R2 = 9 /2 = 4.5A
此时: I3 = (Ua-Ud)/ R3 = -9 / 3 =-3 A
即稳态时:Ua=0v UB = Uc = Ud = 9v I1=0A I2 = 4.5A I3 = -3A
二、1、开关由2指向1的瞬间:我们知道,电路变化前,C1的电压Uba=9V,电管的电流I1=4.5A,所以在开关由2指向1的瞬间,R1、
C1、R2、L形成串联回路,回路电流为4.5A。流向为I2所示的电流方向,流过R1,使Ub = 4.5 * R1 +E2 = 13.5V. 此时
C1的电压Uba 仍=9V,故:Ua = Uab + Ub = -9 +13.5 = 4.5v
而此时Ua又 = Uac + Uc = -4.5*2 +Uc = 4.5v
故可得 : Uc = 4.5 + 9 =13.5v ,而Ud及I3仍保持原来值不变。
2、开关由2指向1稳态后:开关由2指向1,使a点悬浮,C1、L1通过R1、R2放电,直至C1的电压=0,L1的电流=0,即进入稳
态,此时I1 = I2 = 0,故: Ua = Ub = Uc = Ud 而 Ud 及 I3 保持不变,即:
Ua = Ub = Uc = Ud = 9V
I1 = I2 = 0
I3 = -3A
三、 1、开关由2指向3的瞬间:我们知道,电路变化前,C1的电压Uba=9V,电感的电流I1=4.5A,在开关由2指向3的瞬间.Ua=15V
故:Ub = Uba + Ua = 9 + 15 =24V
I1 =(Ud–Ub)/ R1=(9-24)/1 =-15A
Uc = Uca + Ua = 4.5 * 2 +15 =24v I2 = 4.5A
而Ud 及 I3 仍保持原值不变
2、开关由2指向3稳态后:L1相当短路,故 :Uc = Ud =9V
则: I2 = Uca/R2 = ( 9–15 )/1 = -6A
C1相当开路,故:I1 = 0,使Ubd = 0, 所以 Ub = Ud = 9V
此时,Ua=15V,而Ud、I3仍保持原值不变 。
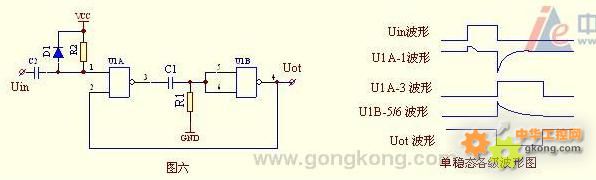
第6题解答:
这是一个由二个与非门与一个RC微分电路组成的单稳态电路。其稳态时,R1的电压=0,故使与非门U1B的输出(4脚)电压=1,使与非门U1A的2脚为1,与非门U1A的1脚由于有上拉电阻R2,其1脚也为1,故与非门U1A的输出3脚电位=0。故电容C1的电压=0。
输入端的R2与C2也是一个微分电路,但由于R2并接二极管D1,使当输入一正方波信号时,其输出波形变为只有一个由1下跳为0的负尖脉冲(与输入方波的后沿同时刻),它使U1A的1脚由1 变0,其输出3脚由0上跳为1,由于C的电压=0,故使U1B的输入5、6脚由0上跳为1,其输出4脚有1下跳为0,此0电压传给U1A的2脚,使输入的负尖脉冲消失后仍能保持U1A输出为 1不变。 随着C1向R1放电,U1B的 5、6脚电位由1逐渐下降,当降到0V时,U1B的输出由0上跳为1,传给U1A的2脚,使U1A的输出由1下跳为0,C通过R2放电直至为0,该电路又恢复原稳定状态。在此变化的过程的各级波形见上图的右侧波形图。
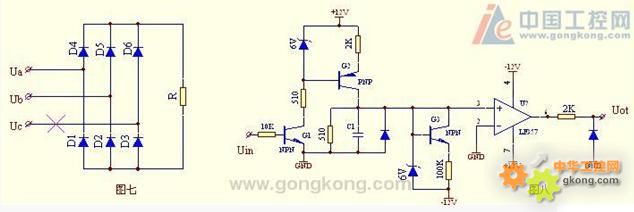
第7题 解答:
见图七:线电压380V的三相电全波整流电路,负载R为纯电阻,正常情况下,R的直流平均电压= 2.34Uo(交流电的相电压)= 2.34 * 220 = 514.8V。
如C相保险烧断,该三相全波整流电路就变成单相桥式全波整流电路,故还能输出直流电流。不过输出的直流电压降低,而且纹波变大。断路的二个整流管D3、D6此时变成串联一起,并接在R的二端,由于其负极接直流输出的正极,故D3、D6处于反向截止状态,对此时的电路工作无影响。如果负载是感性,它们还起续流作用,可提高纹波系数。
由于该单相整流电路的电源电压=380V,故此时R的平均电压 = 380 * 0.9 = 342V
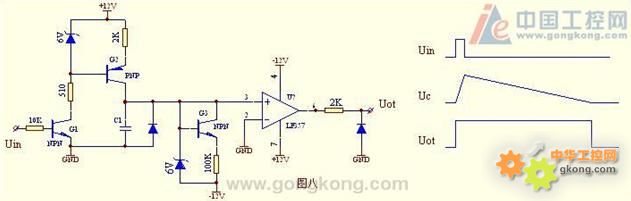
第8题 解答:
图八是脉冲宽度放大器,又叫时间放大器。它可将输入的窄脉冲经过该电路的作用,变成脉宽扩大N倍的宽脉冲。用它可以精确测量窄脉冲的宽度,例如:高精度超声波测厚仪多选用此电路,超声波在钢板中传播速度数匀速的,从发射到接受形成的测厚方波的宽度与被测钢板的厚度成正比,即可用测厚方波的宽度来代表钢板的厚度。如用测量1mm钢板的测厚方波控制计数器的输入,使其在此宽度内,计数器记下100个计数脉冲,则1个脉冲表示0.01mm的钢板厚度,即测厚精度为0.01mm。但1mm测厚方波的宽度=0.34uS,如想在这么窄的宽度计100个数,其计数脉冲的频率要高达近300MHz,用一般的计数器是无法胜任的,如选用时间放大器,将测厚方波脉宽扩大100倍,其计数脉冲的频率用3MHz就可实现0.01的测厚精度。
图八中的电容C1是该电路的核心,对C1放电与充电电流的比,决定了脉宽放大的倍数。我们知道,用恒定电流对C的充电,电容的电压在未达到饱和时,其Uc = I * T /C,式中的I与C是常数,故:Uc与充电时间T成比例。图中的G2、G3分别构成充电与放电二个恒流源,其电流比=100/2=50,即脉宽可放大50倍,其工作原理是这样的:无脉冲输入时,G1截止使G2截止,G2无输出电流向C充电,G3 产生I2电流向C放电,但当C的电压稍变负时,二极管导通,限位C的电压=0,同时比较器LF357输出=0。
当输入一正窄脉冲,G1导通,G2将产生恒定电流I1,此时将以(I1-I2)向C充电,使C的电压有0开始上升,比较器输出由0上跳为1。当输入脉冲结束后,G2的I1=0,此时G3产生的恒定电流I2开始对C放电,当放电到C的电压=0是,比较器输出由1下跳为0,二极管导通限位C的电压=0,电路进入稳态。见图八右图。
把图八的右图贴上来:
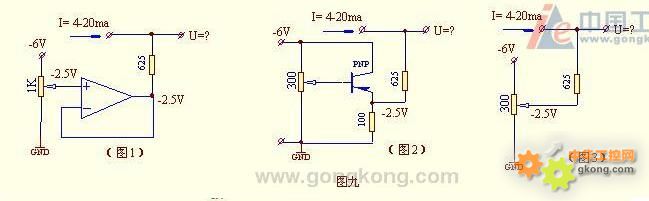
第9题 解答:
4-20ma电流信号流经625欧电阻,会在电阻两端产生2.5-12.5V的电压降,如将电阻的下端接-2.5V的标准电位,其电阻的上端对地电位为0-10V,从而可实现将4-20ma的电流信号转换成0-10V的电压信号。本题的这三种电路就是为提供-2.5V标准电位的,图1与图2是由电压跟随器的输出提供的-2.5V基准电压,当625欧电阻中的电流变化时,其输出点位不变,从而确保转换后的电压输出的正确性。但图3不用电压跟随器,直接将电位器的中间抽头调整为-2.5V,用它直接接625欧电阻,这种电路是不可取的,原因就是它不能提供稳定的-2.5V基准电压:当625Ω电阻无电流时,电位器提供-2.5V电压,根据串联电路电压比=电阻比可知:抽头对地电阻=300×2.5÷6=125Ω.当4ma流入电阻时,其电流也同样流过这电位器的上下部分电阻,使抽头电压由原来的-2.5V发生变化,用戴维南定理可求其等效电源及内阻,即相当是-2.5V电压源又串接72.9Ω,这样当输入4ma电流时,输出电压=4×(625+72.9)-2.5=0.29V, 输入20ma电流时,输出电压=20×(625+72.9)-2.5=11.46V。显然达不到转换为0-10V的目的。图1与图2相比,图1好而图2次之,其原因,图2的晶体管的发射结的电压受温度影响而发生变化,故影响输出电压的精度。
最后修改:2011/5/30 21:26:39