惯量匹配的概念来源于碰撞理论
刘志斌

1、惯量匹配的概念来指哪里？
2、所有现成的文献，都没有一个明确的定义；
3、伺服惯量匹配，显然是个动量传递的问题；
4、仔细分析不难发现，惯量匹配的概念来源于碰撞理论：
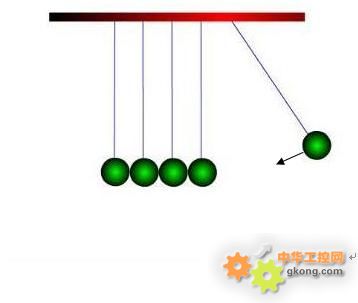
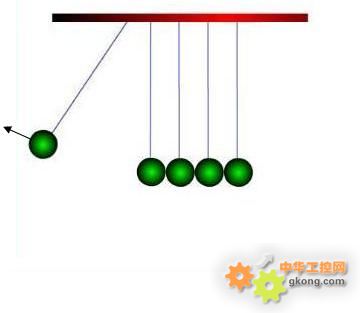
1）如图，质量相等的小球碰撞时，总是将其动量完全传递给另一个小球
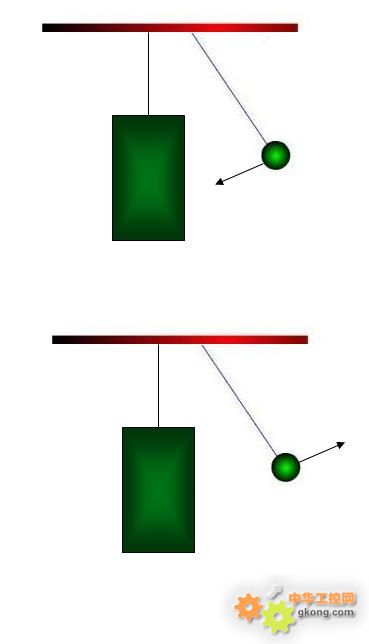
2）一个质量小的球与其质量相比无穷大的物体碰撞时，小球的动量翻转，不仅动量没有传递出去，自身的动量反向，如图
5、这样我们定义：把发生动量传递的两个物体的惯量相等，叫做惯量匹配；把发生动量传递的两个物体的惯量相差无穷大，叫做惯量不匹配。
    认为：惯量匹配时，一个物体的惯量会完全传递给另一个物体；惯量不匹配时，惯量小的物体的动量会反向。

引用 ShowMotion 的回复内容：
……鉴别：风马牛不相及；当然刘老师您认为马和牛都是动物也没错。呵呵。
-------------------------------------------------------------------------------
1、很简单，你没有自己的观点！你也不知道惯量匹配的概念哪儿来的？
2、有一个观点，他说从牛顿第二定律知道，T=Jβ，当转矩一定时，惯量J大时，则角加速度β小，所以惯量大小决定了系统角加速度的大小；
3、还有一个观点说，系统惯量J=JL+JM，当JM大小不同时，JM在系统惯量中的比例不同，从而影响负载的加速度；
4、……


1、我的观点是，实践证明了惯量匹配是动量传递的最佳方式和最佳条件！
2、电机与负载间就是一个动量传递的问题，当系统处于平衡运动状态时，没有惯量匹配的问题；
3、所谓负载惯量是电机惯量的倍数应该是多少？只是惯量匹配原则的一个实际妥协应用问题；
4、我们看不出惯量匹配时，不论是低速运行还是高速运行，不论是起步还是停车，不论是加速还是减速有什么弊端！
5、在辩论中，我也认为电机惯量与负载惯量相等时，系统惯量J=JL+JM增大，在动力矩T一定的情况下，系统加速度受到制约；
6、所以负载惯量是电机惯量的倍数是系统在惯量匹配与系统负载加速度之间的一个妥协实际应用问题！
7、负载惯量是电机惯量的倍数增大时，系统惯量J=JL+JM减小，系统加速度增大；
8、负载惯量是电机惯量的倍数减小时，系统惯量J=JL+JM增大，系统加速度减小；
9、负载惯量是电机惯量的倍数增大时，系统惯量J=JL+JM减小，系统加速度增大；但是远离惯量匹配状态，动量传递不畅性增大；
10、负载惯量是电机惯量的倍数减小时，系统惯量J=JL+JM增大，系统加速度减小；但是靠近惯量匹配状态，动量传递流畅性增大；
11、如果负载惯量是电机惯量的倍数减小时，同时选用额定转矩T大的电机，既不减小系统加速度，又能使系统接近惯量匹配状态，也是一种选择！

12、各种机加工项目的要求、特点我不清楚，所以我不能给你提供负载惯量是电机惯量的倍数是多少，但是我给了你选用这些倍数大小的方向，知道这个方向，你就可以灵活应用，不致受骗、受人利用！

13、例如，你在系统设计中，选用了计算转矩的5/3倍的电机，转矩富裕，这时候你就可以将那个倍数5选小到1也可以，这样可以直接确定系统的
       最佳传动比的平方=负载的惯量/电机的惯量

1、五个小球的惯量相等，右边一个小球的动量瞬间传递给左边小球，就好像小球自己摆过去的一样，所有小球没有收到任何冲击，动量被完全传递！
2、这种物理现象我们称系统惯量匹配，惯量匹配动量能完全得到传递，所有物体都不受冲击，安全、可靠、稳定。
3、你看，如图，一个惯量相比无穷大的两个物体相碰，惯量小的小球把自己给碰飞了！
4、这就是惯量不匹配，惯量不匹配，不仅动量传不出去，而且受冲击或被损坏的是惯量小的一方！
5、要注意，只有系统内处于非平衡状态时，系统内各部分之间存在相对运动，存在相互作用力时，即存在动量传递时，才有惯量匹配的问题！
6、如果忽略系统内力的作用，把系统看成一个刚性整体，则不存在惯量匹配的问题；
7、或者系统处于平衡运动状态，如匀速直线运动状态、或匀速圆周运动状态，就没有惯量匹配问题；
8、不能把非惯量传递问题说成惯量传递的问题，也不能把惯量传递的问题说成非惯量传递的问题；
9、例如，当我们把这几个小球看成一个加速度相同的整体时，当外力F一定时，能使系统获得的加速度大小与小球的个数成反比，这时候没有惯量匹配的问题！
     F=5ma
     a=F/5m
10、这时候，是个纯粹的牛顿定律的问题！没有动量传递的惯量匹配问题！

先把慣量定義搞清楚 就不會在此胡扯
剛性連結所造成的傳動竟讓你說成碰撞
慣量的匹配是存在整個系統內 彼此透過剛性連結 要動一起動 要停一起停 純在瞎扯 五個鋼珠的圖我只看到位能變動能 能量傳遞 動能變位能
還有很多錯 懶得幫你寫 你這個扶不起阿斗 哀

“五個鋼珠的圖我只看到位能變動能 能量傳遞 動能變位能”
1、那右边的球瞬间停止速度为零，它的动量传到哪儿去了？
2、你没有看见动量由右边小球传给左边小球？

“整個系統內 彼此透過剛性連結 要動一起動 要停一起停”
1、“整個系統內 彼此透過剛性連結 要動一起動 要停一起停”，那就只有整体的1个惯量，整体只有牛顿定律的问题！
2、如果“整個系統內 彼此非剛性連結 要動不一起動 要停不一起停，存在一部分对另一部分的相对运动和内力，就有各部分间惯量匹配的问题；

很多的时候，传动系统的驱动轴连接也不都是刚性的连接，更多的时候是弹性连接，不论是法兰式的，还是万向节式的，有弹性材料作缓冲的。其实，楼主说的问题，在控制上完全作为一种思路，可以尝试。
当然，作为技术的讨论是自由的，大家各抒己见，无可厚非，都有自己的观点嘛，只是千万别搞成相互的个人攻击就好。

转动惯量不是与物体的重量成正比的，而是与质量分布有关的；

引用 ZCMY 在 2012/12/24 11:07:19 发言【内容省略】

1、物体平动时，惯量就是物体的质量；
2、物体做转动时，惯量就是你说“与质量分布有关”的惯量；
3、例如那几个质量相等的小球，可以看成平动，也可以看成转动，平动时的惯量就是质量m，转动时的惯量就是mr^2!